|
|
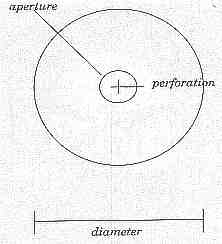
The starting point for describing beads is the perforation. The opening of the perforation is the aperture.
Perforations are very important.
Looking through the perforation gives you the cross section of the bead. The widest part of the cross section is the diameter.
|
|
The axis of the bead runs through the perforation. Looking at the axis gives you the profile of a bead. The length of the axis is usually the length of the bead.
|

|
|

|
Beads may be described by referring to their cross section followed by their profile. This bead would be a round barrel. In practice, with beads of round sections, "round" is eliminated.
Thus, this is a barrel bead.
|
|
Beads are actually three-dimensional objects. It is common to speak of them in a combination of two (the cross section) and three dimensions. This bead is a hexagonal tube or hexagonal prism.
|

|
|

|
Two cones joined at the base form a bicone. If the length is + 25% of the diameter, it is called "standard," a term often not mentioned. Long and short beads deviate from this norm. Faceted bicones may be hexagonal bicones, square bicones, etc.
|
|
A bead with round cross sections and profiles would be a sphere, as is this one. In the real world, most round beads have at least slightly flattened ends and are better called oblates. Those very flattened are suboblates.
|
|
|

|
A special type of bead is called a tabular, because it is a flat bead (like a table top) that has been pierced through a long axis. Tabulars are then described by the shape of their flat face; this is a round tabular.
|